Circumference of a circle

The distance around the perimeters of a circle is known as the circumference of a circle. The length of the edge around a circle is known as the circumference of the circle. To further understand this notion, consider the following diagram. Consider the example of a circular playground in the diagram below.

A route is covered by a player if he runs from point A to point B after a complete round of the playground. The distance covered by a player is called the circumference of the playground. The circumference is presented by the letter C in mathematics. It has units of measurement such as centimeters (cm),millimeters(mm), and inches(in).

A circle’s circumference is its perimeters. The equation for determining a circle’s circumference

Circumference of a circle = π×d

C = π×d

C = 2πr

The following equations relate it to its diameter, radius, and pi. “C” stands for the circumference of the circle “d” is the diameter of the circle.“ π” is constant and the special number is equal to 3.14519…. or 22/7. A circle’s diameter is the largest distance across it can be measured from any point on the circle, passing through its center, to the point of interconnection on the opposite end. The radius is half the diameter.
Looking for math homework help? Our experienced tutors can provide comprehensive assistance with understanding and solving equations, including those related to circles and geometry.

The radius 'r' of a circle and the value of 'pi' are used in the formula for calculating the circumference of a circle. Circumference of a circle formula = 2r is one way to express it. If we don't know the radius value, we can use the diameter to find it using this circumference formula. Because the diameter of a circle equals two radii, if the diameter is known, it may be divided by two to obtain the radius value. Circumference = Diameter is another formula for calculating a circle's circumference. When the circumference of a circle is given, we apply the formula Radius = Circumference/2 to determine the radius or diameter of the circle.

The circumference of a circle is the length of its boundary, it cannot be determined with the help of a scale-line. This is attributable to the fact that a circle is a curvy figure. Therefore, we calculate the circumference of the circle with the help of the circumference formula.

Circumference of a circle=π diameter

C=π×d

Example: What is the circumference of a circle whose diameter is 13 units?

Solution: Given diameter = 13 units

Let us use the circumference formula and substitute the value of diameter in it.

Circumference of circle formula=π×d

C=π×d

C=3.14×13

C=40.82 units

Hence, the circumference of a circle is 40.82 units.

Problem: Lauren is planning a trip to London and wants to ride the London Eye, the world's most famous Ferris wheel. She discovers the radius of the circle measures around 78 meters while investigating details about the enormous Ferris wheel. What is the Ferris wheel's estimated circumference? As a rough estimate of pi, use 3.14.

Solution:

The Ferris wheel has a radius = of 78 m

Ferris wheel’s circumference = ?

Using circumference formula

Circumference of ferries wheel = 2 π  r

C =3.14

C= 489 m

Although the circumference of a circle is proportional to the length of its boundary, it cannot be calculated using a ruler (scale) like other polygons. This is attributable to the fact that a circle is a curvy figure. As a result, we utilize a formula that uses the radius or diameter of the circle and the value of Pi () to calculate the circumference of a circle. When tackling geometry problems involving circles, understanding how to use the formula for calculating the circumference is essential for successful completion of your coding assignment.

The below equation explain the relationship between the circumference and the radius of a circle

c=2πr

Where is a constant and has a fixed value which is equal to 3.14159265..... The exact figure is impossible to calculate. We generally use approximations like3.14 or 22/7 because it’s an irrational number.

Method to calculate the circumference of a circle

Method 1: Using diameter to calculate the circumference of a circle:

Use the formula

C=π×d

If we know the diameter we can determine the circumference. In this relation, "C" symbolizes the circumference of a circle, and "d" symbolizes its diameter. That is to say, we can find the circumference of a circle just by multiplying the pi by diameter. Substituting the value the numerical value is 3.14 or 22/7.plug the given value of the diameter into the circumference formula and solve. For further practice examples problem below:

Example: A circular bike wheel with a diameter of 10 feet. Calculate the circumference of a circular bike wheel.

To calculate the circumference of the circular bike wheel. The diameter of thecircular bike wheel is 10 feet. Now substituting the values in the formula

C=π d

C=π×10

C=31.42feet

Method 2: Using radius to calculate the circumference of a circle:

Use the formula

C=2πr

This relation represents the radius of the circle.

A radius is the length of the line segment from the center of the circle to its other endpoint on the boundary of the circle.

This formula is similar to C=π d. That's because the radius is half of its diameter, so the diameter can be written as d=2r.

Substitute the given radius value into the above relation and solve it. For further practice examples problem below:

Problem: You are cutting out the ribbon to wrap around the edge of the bangle. The radius of the bangle is 2 inches.

Solution: To calculate the circumference that you need just, putting the values of radius in a given equation

C=2πr

C=2 π 2

C=12.57inches

We would know either the diameter or the radius of a circle to calculate its circumference. Then, in this equation, we utilize the proper value: C=2πr (of course, "r" stands for radius).

As we know, the formula for finding the circumference of a circle equals pi time diameter.

C=π d

Just like, more formulas we use abbreviations: C for circumference and d for diameters. That's a pretty simplest formula. It tells us that if we know the diameter of a circle, all we have to do is multiply the diameter.

Problem: A circular rug has a diameter 46m.what is the circumference of a circular rug?

Solution: 

Circular rug’s diameter =   42 m

Circumference of a circular rug=?

By using the circumference formula

Circumference of a circular rug = π

Circumference of a circular rug = π

 Circumference of a circular rug = 132 m

Problem: Johan drove the car. His car wheel has a diameter is 4 m. Find the distance covered when it completes 50 revolutions?

Solution:

Firstly, to find the distance covered in 1 revolution, we have to find the circumference of the wheel.

The radius of wheel = diameter of wheel/2

=4/2=2 m

Distance covered when 50 revolutions are completed = 50 circumference of the wheel

=50

=50

=616 m

Eratosthenes was the first person who measures the circumference of Earth. He was a Greek mathematician, in 240 B.C. He discovered that objects in a city on the Northern Tropic don’t throw a shadow at noon on the summer solstice, but they do in a more northerly location. By knowing this and the length between the locations, he succeeded in measuring the Earth's circumference. The distance between the two cities was measured by Eratosthenes to be 800 kilometers. He multiplied 800 kilometers by 50 to arrive at a figure of 40,000 kilometers for the Earth's diameter.

Even though the circumference of the circle is its length, it cannot be measured using a scale like other shapes like squares, triangles and rectangles can the rationale for this is the circle's bent shape.

The strategies below can be used to measure the circumference of a circle

Method 1. We would use this thread to trace the course of the circle and designate the places on the trend a common Ruler can be used to check the thread length later. Study the possibility when we are given a circular plate with a circumference of a circle. 

Step 1. Using the method described above, we could now take a thread and wrap it towards the circular plate.

Step 2. Next, on the thread, make a starting and ending point.

Step 3. Finally, using the perimeter measurement, measure the length of the thread from start to finish point.

Method 2. Measuring the circumference of a circle is an accurate way to calculate it in geometry. As a result, we apply a formula that involves the radius, diameter of a circle, and the value of Pi(π) to determine the circumference of a circle. To the beginning, if we are given the radius and circumference must be computed, the steps to follow are as follows:

If the radius of any random circle is 7 cm, we may determine the circumference using the following steps:

Step 1. Check over the data which have been provided to us; in this case, the radius has been provided.

Step 2. Use the following formula

C=2πr

Here C = circumferences, r= radius, and π=22/7.

Step 3. We obtain the desired outcomes by substituting values in the formula

Step 4:

C=2π r=2 22/7 7=44cm

Similarly, if the diameter is specified, we can follow the procedure below:

Example: If the diameter of circular CD is given as 14cm and the circumference is required, the following is the solution:

Step 1. Check the given information, in this case, diameter is given.

Step 2.Use the following formula

C=π d

(Here, C denotes circumference, d denotes diameter, and π=22/7 or 3.14)

Step 3.We get the required result by substituting the values in the formula.

C=π =22/7 14=44cm

Circumference of a circle is the distance around the circle and the diameter over circle is the line segment of a circle is the line segment used and point lies on the circle and that pass through the center of the circle so yellow lines in the diagram will be the diameter of the circle because gives and points lies on the and it passes through the center of the circle so a line segment like this is called the diameter of the circle.

Circumference to diameter:

The ratio of circumference to diameter is derived from the conventional definition of Pi (π).

C=π d

Eliminate d by both sides

C/ d=π

We can get a value that is proximately comparable to both sides of the equation

(C=π d) by the diameter d. C represents circumference and d represents diameter.

This indicates that

d=C/π

We can use it to find diameter if we know circumference since circumference and diameter are related by Pi (π). To isolate diameter d, on one side of the equation, we conduct some math:

C=π d

C/π = d

The diameter is then determined by dividing the circumference by Pi (π).

we understand this concept by an example:

Example: A Dome of a building is surrounded by a 63-foot-circumference circle. The Dome of a building has a diameter of what?

Solution

Circumference of Dome = 63 feet

Diameter of Dome=?

By using a circumference formula

C=π d

d=C/π

d=

d= 20.06feet

The pitcher's mound circle has a diameter of 20.06 feet.

If we know the diameter, we can use the above relation to get the circumference.

Understand this concept with some problems:

Problem: The distance around the equator of Uranus is about 160.535 km. what is the equatorial diameter of Uranus?

Solution:

Step 1. According to the given data,

Uranus’s circumference=160.535km

Equatorial diameter of Uranus =?

Step 2:The formula used in this problem is

d=C/π

Step 3: Substituting the values in formula

d=160.535/π=51100km

Step 4: as a result, the equatorial diameter of Uranus is 51100km.

Problem: A circular swimming pool has a diameter of 7 yards. Work out the circumference of the circular swimming pool?

Solution:

Step 1: Write the given data

Circular swimming pool’s diameter =7 yards

Circumference of a circular swimming pool=?

Step 2: The formula used in this problem is

C =π d

Step 3:Substituting the values in the formula

C=22/7

C=22 yards

Step 4:

Hence, the circumference of a circular pool is 22 yards having a diameter of 7 yards.

We can find the radius of a circle by measuring the distance from its center to its outside edge. Consider a clock: if one of the hands was long enough to reach the edge of the dial, this hand could be considered the clock's radius – regardless of the time!

The diameter of a circle is measured from edge to edge and cuts through the center, whereas the radius is measured from center to edge. The diameter of a circle divides the shape in half. The radius of a circle is half the length of its diameter (or the diameter of a circle is twice the radius).

The radius of a circle is defined as the length from the center of the circle to any point on the circle boundary line of a circle.

As we know that the diameter is twice the length of the radius. Mathematically, it is written as

Diameter=2×radius

D=2r

Circumference of circle is also written as

Circumference of a circle=π d

By substituting

C=2πr

Example: What is the circumference of a circle having a radius of 10units?

Solution: Given radius=10 units

By using formula

Circumference of circle formula=2πr

C=2πr

C=23.1410

C=62.8units

Hence, the circumference of a circle is 62.8 units.

Another important ratio, radius to diameter, can also be used to calculate the circumference. One-half of a circle's diameter is known as the radius. As a result, we may use the replacement attribute of equality to replace radius, r, in our formulae. We can substitute diameter with 2r if two radii are equivalent to one diameter.

The commutative property of multiplication allows us to transfer values around as well. The following four equations are interchangeable:

C= π d

C = π (2r)

C = 2 πr

Understand this concept by practice with an example.

Example: A national team field's striking circle is a quarter-circle with a 32-yard radius, followed by a four-yard straight line and another quarter circle. Two of these eye-catching circles can be found on the pitch. You only have enough chalk left to form a 222-yard line after marking all the straight lines with chalk.

Solution:

Add the two, four-yard straight sections to the circle's circumference to get the total length.

Consider your options before taking a glance!

Four quarter-circles equal one 32-yard-radius circle. Then, for the two straight sections, add sixteen yards.

C=πd

C=2πr

C=2 x 3.14159 x 32yards

C = 2 x 3.14159 x 32 yards

C = 200.96 yards

Combine the two following: 200.96 yards+ 16 yards=216.96 yards

A circle is the set of all points in a plane that are a fixed distance from a fixed point, called the center, and are separated by a fixed distance, called the radius. A circle's perimeter, or distance around it, is its circumference (C). A circle's area (A) is the amount of space it occupies or the area it encompasses.

Calculate the area of a circle by using the formula:

Step 1. The area of a circle can be determined using two distinct formulas based on the diameter or radius:

A =π or A = π , where is a mathematical constant of about 3.14.’ r‘ is the radius, and ‘d’ seems to be the diameter.

These equations are essentially the same because the radius of a circle is equal to half of its diameter. The area can be measured in feet squared ( ), meters squared ( ), centimeters squared ( ), and other units of length squared.

Step 2. Recognize the various components of the formula. The radius, diameter, and circumference of a circle are the three components needed to calculate its circumference. The radius and diameter are proportional: the radius is half the diameter, and the diameter is double the radius.

A circle's radius (r) is the distance between one point on the circle and its center.

A circle's diameter (d) is the distance between one point on the circle and another exactly opposite it, measured through the center.

The number 3.14159265..., an irrational number with neither a final digit nor a recognized pattern of repeated digits, shows the ratio of circumference divided by diameter.

Step 3.Calculate the circle's radius or diameter. Place one end of a ruler on one side of the circle and the other end on the other side of the circle, passing through the center point. The radius is the distance from the circle's center, while the diameter is the distance from one end to the other.

The radius or diameter is provided radius=4m diameter=6m

Step 4. Solve the problem by putting in the variables. You can put the radius and/or diameter of the circle into the relevant equation once we've determined the radius and/or diameter.

Use A =π  if you know the radius, but A = π  if you know the diameter.

Example: What is the area of a 4 meter radius circle?

By putting the values:

A =π  is a formula that describes the relationship between two variables.

Variables to the plugin: A=π

Radius is squared: The  value is  which equals sixteen.

Multiply by pi (π) if we want to get a more complicated answer

A=π  16 =

Example:

What is the area of a circle with a diameter of 8 meters?

By putting the values

A =π  is a formula that describes the relationship between two variables.

Variables to the plugin: A=π

By multiplying the diameter by two, you can arrive at the following result:2 =8

= 64is the squared result.

Multiply by pi (π) if we want to get a more complicated answer

A=π 64=200.96 meters

Calculate the Area and Circumference of a circle with variables:

Step 1.Calculate the circle's radius or diameter. Some issues will offer you a variable radius or diameter, such as r = (y+ 2) or d = (y+ 4). You can still solve for the area or circumference in this scenario, but your final solution will include that variable. As specified in the problem, write down the radius or diameter.

As an illustration: Determine the circumference of a circle with (y = 2) radius.

Step 2.With the information provided, write the formula.

Regardless of whether you're solving for area or circumference, the essential steps of filling in what you know will remain the same. Make a note of the area or circumference formula, and then put in the variables.

As an illustration: Compute the circumference of a circle with a radius of (y +2) and a diameter of (y + 4).

Write the formula: C =2πr

Fill in the details with the provided data: C=2π(y+2)

Step 4.Solve the problem as if the variable was a number. You can now answer the problem normally, using the variable as if it were a number. To simplify the final answer, you may need to apply the distributive property.

As an illustration: Calculate the circumference of a circle with a radius of y=1

C = 2πr=2π(y +2) = 2πy +2π(2) = 6.28y + 12.56

You can insert the value of "y" in the above equation to obtain a whole number solution.

C = 6.28 (1) + 12.56 =18.84 units

The region surrounded by the circle itself, or the region covered by the circle, is called the area of a circle. The area of a circle on a two-dimensional surface is the area occupied by the circle.. The area of a circle can be calculated using the following formula:

A=π

This formula applies to all circles of varying radii, where r is the radius of the circle. The square unit, such as ,  and so on, is the unit of area.

The area of the circle formula can be used to calculate how much space a circular field or plot typically takes. If you have a plot and want to fence it, the area formula can help you figure out how much fencing you will need.

If we know the radius of a circle, finding its area is a simple computation. If we don't know the radius, we can still determine the area if we know how long the circumference or perimeter of the circle is. We can solve for the radius first, then the circumference, using the formula

Circumference = 2πr

The area may then be calculated using the formula

Area of a circle=π

We can also use the formula

Circumference=

 We can find the radius of a circle by dividing its area by and then taking the positive square root, as shown by the formula

 A = π

A/π =

= r

Without knowing the length of the radius, this expression expresses the circumference of a circle as a function of its area.

Understand that area is the amount of space covered by a two-dimensional figure, and it's expressed in units squared. The area of most forms, including circles, must be calculated using a formula. Use the following formula to find the area of a circle:

A = π

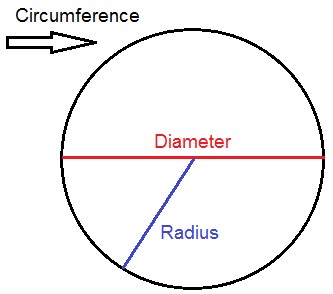
The radius of a circle is shown in green while the diameter of a circle is shown in red. These are necessary for computing a circle's area.

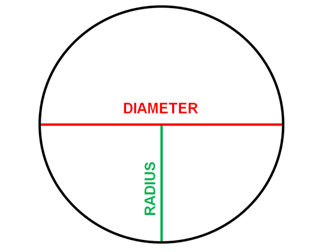
The diameter and radius of a circle are used to calculate its area.

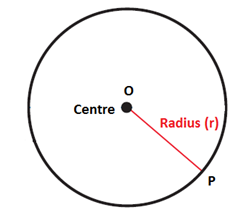
The radius, or a segment from the circle's center to a point on the circle's edge, is represented by the letter r in this formula. It's half as big as the diameter, and every radius inside a circle is the same size. Let's explore how to find the area of a circle in more detail.

Determining a Circle's Area Problem:

Consider now at circle M:

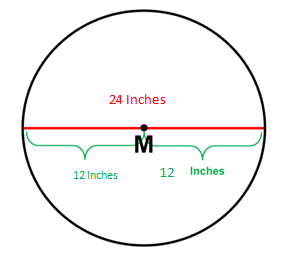
M's radius is half its circumference. M's area is calculated using its diameter and radius.

The diameter is 24 inches long, as may be seen above. To find the radius and calculate the area of circle M, we must divide the diameter in half. We can see that the radius is 12 inches long when we divide 24 by two.

Radius=diameter/2

r=d/2

r=24/2

r=12 inches

For calculating the area, we use the formula

A=π

We'll add radius= 12 to the equation now:

A=π

A = π 144 = 452.16

is a formula that can be used to calculate several things.

Let's consider the example from actual life.

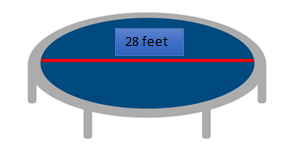
The area of this dining table may be determined using the red line that runs through the center.

The dining table's diameter is used to calculate the area of the circle it symbolizes.

John is buying the materials he'll need to create his first dining table. How much wood will he need to acquire if he wants the table’s diameter to be 28 feet long?

Solution:

To determine the radius, we'll reduce the diameter in half once again.

Radius= diameter/2

r=d/2

r=28/2

r=14 feet

The table's radius will be 14 feet when you're done. After that, we plug this radius into the equation:

A=π

A=π  =196 π

A=616

The overall area of the dining table is 196π, or 616 feet squared, once we complete our calculations using the order of operations.

Exploring the relationship between area and circumference:

Begin with a circle of radius r.

The formula for determining the circumference and area of a circle with radius r is well-known.

C = 2πr in circumference

Area

A = π

1st step:

For r, solve the equation C = 2πr

Both sides divided by 2π

C/2π= 2πr/2π

C/2π =r is a mathematical expression that expresses the relationship between two variables

2nd step:

In the formula for circle area, substitute r = C/2π

A = π

Within the brackets, square the terms.

A = π

Simplify

A =

A =  is a formula for calculating the area of a circle.

3rd step:

For , solve the given equation.

Add 4π to both sides of the equation.

4πA = 4π

4πA =

Simplify

  = 4πA

As a result, the circle's radius squared equals four times the area.

Observe

Is this formula applicable to a circle with a radius of 14inchs? Put your work on display.

We can apply the formula = 3.14 because the radius of  14 inches is a multiple of 7.

First, we must complete the following steps.

Calculate the circle's surface area.

is a formula that describes the relationship between two variables.

Put r = 14

A = π

π replace by

A=  196

A = 616

2nd step:

Measure the circle's circumference.

C = 2π r

Put r = 14

C = 2 π  14

C = 2

C=88 inches

Step 3:

Make the circle's circumference square.

 =  =7744   ————— (1)

By multiplying the area by 4π, you can get a more accurate estimate of the size of the region.

A = 616

4π A = 4π

4π A = 4

4π A = 7744   ——————— (2)

We can conclude from (1) and (2)

  = 4πA

As a result, the area is four times the circumference of the circle squared.

Example: A rectangular wire has a 132-meter perimeter. A circle is formed by twisting the same wire. The circumference formula can be used to calculate the radius of a circle.

Solution:

The perimeter of the rectangle equals the total length of the wire utilized, which equals the circumference of the circle produced.

As a result, the circle formed has a circumference of 132 meters.

The formula for calculating the circumference of a circle = 2 πr

132 is the circle's circumference.

To find the radius, we can substitute the known values.

132 = 2r

132 = 2 (22/7) r

132 = 44/7 r

= r

r = 21 meters

Thus, the circle's radius is 21 meters.

Understand this concept by using an example:

Example: Umar completed four laps of a circular track. What is the diameter and radius of the field if he ran a total distance of 500 m?

Solution:

Umar completed one laps of circular field = 500 / 4 =125

The circumference of a circular field is 125 meters.

Diameter of circular field = circumference / π

Diameter of circular field = 125/3.14= 39.81meters

Radius of circular field = circumference / 2π

Radius of circular field = =  = 19.905 meters

Example: Circular parks have a 70-meter diameter. At $2 per meter, calculate the cost of fencing it.

Solution:

The park has a 70-meter diameter.

The radius of the circle is

r= 70/2 = 35metres

A meter of fencing costs $2.

The circumference of the circular park is the length covered by fencing.

The park's circumference is

=2 π r

= 2 (22/7) x 35 = 220 meters

Fencing has a cost = 220  2 =440 dollars

Example: On one of his new apartment's walls, Jasmin is painting a big circle. The circle will be 49 feet in diameter at its widest point. What is the approximate area that the circle will cover on a wall?

Solution:

We are finding an area if you are asked to calculate the number of square feet covered by something. To calculate the area of Jasmin's circle, we must first determine if the radius or the diameter has been given. The diameter of a circle is defined as the longest distance across it, hence the diameter is 49 feet in this case. The radius is 7 feet in this case. Therefore:

A= π   = 154

As a result, Jasmin's circle will encircle approximately 154 square feet of his property.

Example: A birthday party was held in a circular lounge. The diameter of the circular lounge is 14 yards. What is the area of the circular lounge?

Solution:

The diameter of circular lounge = 14 yards

We want to find the area of the circular lounge

Firstly we will find the radius of a circular lounge from diameter, as we know

Radius = diameter/2

r = 14/2 = 7 yards

By applying the circle’s area formula

= 154 yards

As a result, the area of the circular lounge is 154 yards.