How to find area of a circle with circumference
The region surrounded by the circle itself, or the region
covered by the circle, is called the area of a circle. The area of a circle on
a two-dimensional surface is the area occupied by the circle.. The area of a
circle can be calculated using the following formula:
A=π
This formula applies to all circles of varying radii,
where r is the radius of the circle. The square unit, such as
The area of the circle formula can be used to calculate
how much space a circular field or plot typically takes. If you have a plot and
want to fence it, the area formula can help you figure out how much fencing you
will need.
If we know the radius of a circle, finding its area is a
simple computation. If we don't know the radius, we can still determine the
area if we know how long the circumference or perimeter of the circle is. We
can solve for the radius first, then the circumference, using the formula
Circumference = 2πr
The area may then be calculated using the formula
Area of a circle=π
We can also use the formula
Circumference=
We can find the radius of a circle by dividing
its area by and then taking the positive square root, as shown by the formula
A = π
A/π =
Without knowing the length of the radius, this expression
expresses the circumference of a circle as a function of its area.
Understand that area is the amount
of space covered by a two-dimensional figure, and it's expressed in units
squared. The area of most forms, including circles, must be calculated using a
formula. Use the following formula to find the area of a circle:
A = π
The radius of a circle is shown in green while the diameter of a circle is shown in red. These are necessary for computing a circle's area.
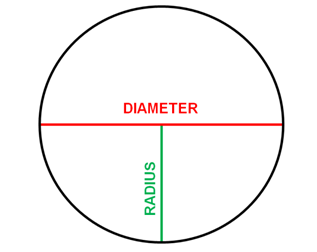
The diameter and radius of a circle
are used to calculate its area.
The radius, or a segment from the
circle's center to a point on the circle's edge, is represented by the letter r
in this formula. It's half as big as the diameter, and every radius inside a
circle is the same size. Let's explore how to find the area of a circle in more
detail.
Determining a Circle's Area Problem:
Consider now at circle M:
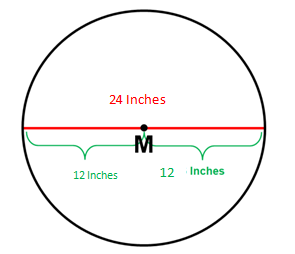
M's radius is half its
circumference. M's area is calculated using its diameter and radius.
The diameter is 24 inches long, as
may be seen above. To find the radius and calculate the area of circle M, we
must divide the diameter in half. We can see that the radius is 12 inches long
when we divide 24 by two.
Radius=diameter/2
r=d/2
r=24/2
r=12 inches
For calculating the area, we use the formula
A=π
We'll add radius= 12 to the equation
now:
A=π
A = π
is a formula that can be used to calculate several things.
Let's consider the example from actual life.
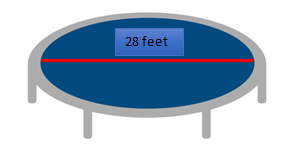
The area of this dining table may be
determined using the red line that runs through the center.
The dining table's diameter is used
to calculate the area of the circle it symbolizes.
John is buying the materials he'll
need to create his first dining table. How much wood will he need to acquire if
he wants the table’s diameter to be 28 feet long?
Solution:
To determine the radius, we'll
reduce the diameter in half once again.
Radius= diameter/2
r=d/2
r=28/2
r=14 feet
The table's radius will be 14 feet
when you're done. After that, we plug this radius into the equation:
A=π
A=π
A=616
The overall area of the dining table
is 196π, or 616 feet squared, once we complete our calculations using the order
of operations.
Exploring the relationship between
area and circumference:
Begin with a circle of radius r.
The formula for determining the
circumference and area of a circle with radius r is well-known.
C = 2πr in circumference
Area
A = π
1st step:
For r, solve the equation C = 2πr
Both sides divided by 2π
C/2π= 2πr/2π
C/2π =r is a mathematical expression
that expresses the relationship between two variables
2nd step:
In the formula for circle area,
substitute r = C/2π
A = π
Within the brackets, square the
terms.
A = π
Simplify
A =
A =
3rd step:
For
Add 4π to both sides of the
equation.
4πA = 4π
4πA =
Simplify
As a result, the circle's radius
squared equals four times the area.
Observe
Is this formula applicable to a
circle with a radius of 14inchs? Put your work on display.
We can apply the formula = 3.14
because the radius of 14 inches is a
multiple of 7.
First, we must complete the
following steps.
Calculate the circle's surface area.
Put r = 14
A = π
π replace by
A=
A = 616
2nd step:
Measure the circle's circumference.
C = 2π r
Put r = 14
C = 2 π
C = 2
C=88 inches
Step 3:
Make the circle's circumference
square.
By multiplying the area by 4π, you
can get a more accurate estimate of the size of the region.
A = 616
4π A = 4π
4π A = 4
4π A = 7744 ——————— (2)
We can conclude from (1) and (2)
As a result, the area is four times
the circumference of the circle squared.